แบบจำลองฮาร์โมนิกส์ที่สภาวะคงตัว (Steady-state harmonic model) ใช้วิเคราะห์ปริมาณแรงดันฮาร์โมนิกส์และกระแสฮาร์โมนิกส์ที่ความถี่ต่างๆเมื่อมีแหล่งกำเนิดฮาร์โมนิกส์ต่ออยู่ในระบบไฟฟ้า รวมถึงวิเคราะห์การเกิดเรโซแนนซ์ของคาปาซิเตอร์ที่ต่ออยู่ในระบบไฟฟ้าตามการเปลี่ยนแปลงของค่ากำลังไฟฟ้าลัดวงจร (Short Circuit Capacity) โดยเปลี่ยนค่าอิมพีแดนซ์ของระบบไฟฟ้าของการไฟฟ้าท้องถิ่น
จากการวิเคราะห์การเกิดเรโซแนนซ์ในกรณีที่ต่อคาปาซิเตอร์ขนาด 12.7 MVAR เข้ากับเมนบัส 12 kV พบว่าจะเกิด Parallel resonance ขึ้นที่ความถี่เรโซแนนซ์ใกล้กับฮาร์โมนิกส์ลำดับที่ 4.7 โดยจะเกิดแรงดันไฟฟ้าสูงสุดตามรูปที่ 4 แสดงว่าต้องติดตั้งฮาร์โมนิกส์ฟิลเตอร์เพื่อกรองฮาร์โมนิกส์ที่ความถี่นี้ (Tuned Harmonic)
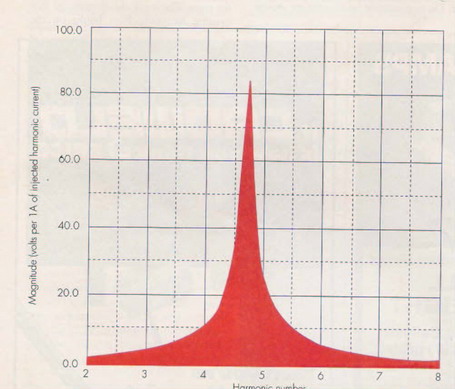
รุปที่ 4 แสดงการเกิดปรากฏการณ์เรโซแนนซ์ชนิด Parallel ขึ้นเมื่ออต่อคาปาซิเตอร์ขนาด 12.7 MVAR เข้ากับเมนบัส 12 kV ทำให้เกิดแรงดันไฟฟ้าสูงสุดใกล้กับฮาร์โมนิกส์ลำดับที่ 4.7 เพื่อแก้ไขปัญหานี้จึงต้องติดตั้งฮาร์โมนิกส์ฟิลเตอร์เพื่อกรองฮาร์โมนิกส์ลำดับที่ 4.7 ที่เกิดขึ้นในระบบ
สมการต่อไปนี้ใช้คำนวณหาขนาดของรีแอกเตอร์ที่ต่ออนุกรมกับคาปาซิเตอร์เพื่อเปลี่ยน Pure Capacitance ขนาด 12.7 MVAR เป็นฮาร์โมนิกส์ฟิลเตอร์ลำดับที่ 4.7 โดยมีวงจรไฟฟ้าของฮาร์โมนิกส์ฟิลเตอร์ลักษณะต่างๆ ตามรูปที่ 5
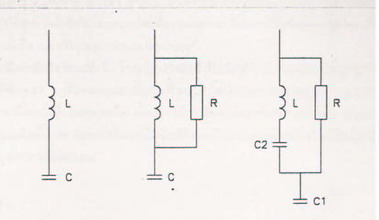
รูปที่ 5 แสดงฮาร์โมนิกส์ฟิลเตอร์ประเภทต่างๆ ตามลักษณะของรีแอกเตอร์
h2 = Xc / XL --------------------------------- (1)
XL = Xc / h2 --------------------------------- (2)
Xc = (kVL-L)2 / MVAR 3-Phase --------------------------------- (3)
โดยที่
h = Tuned Hamonic
Xc = ค่าคาปาซิทีฟ รีแอกแตนซ์ของฮาร์โมนิคฟิลเตอร์
XL = ค่าอินดักทีพ รีแอกแตนซ์ของฮาร์โมนิคฟิลเตอร์
kV L-L = แรงดันไฟฟ้าระหว่างเฟสของชุดคาปาซิเตอร์
MVAR 3-Phase = พิกัดกำลังไฟฟ้ารีแอกทีฟของคาปาซิเตอร์
วิธีคำนวณ
(1) หาค่า Xcโดยแทนค่า kV L-L = 12 kV และ MVAR 3-Phase = 12.7 MVAR ลงในสมการที่ 3
Xc = (12)2 / 12.7
= 11.339 โอห์ม
(2) หาค่า XL โดยแทนค่า Xc = 11.339 โอห์ม และ h = 4.7 ลงในสมการที่ 2
XL = 11.339 / (4.7)2
= 0.513 โอห์ม
เมื่อเปลี่ยนคาปาซิเตอร์ชนิด Pure Capacitance เป็นฮาร์โมนิกส์ฟิลเตอร์ลำดับที่ 4.7 แล้วคำนวณค่าความเพี้ยนฮาร์โมนิคส์รวมใหม่จะได้ค่าดังนี้
1. ค่าความเพี้ยนฮาร์โมนิคส์รวมของแรงดันไฟฟ้าสูงสุด (%Voltage Harmonic distortion) เท่ากับ 2.63% ของแรงดันไฟฟ้าที่ความถี่มูลฐาน (มาตรฐาน IEEE ยอมรับได้ที่ 5%)
2. ค่าความเพี้ยนฮาร์โมนิคส์รวมของกระแสไฟฟ้า (%Current Harmonic distortion) เท่ากับ 3.83% ของกระแสไฟฟ้าที่ความถี่มูลฐาน (มาตรฐาน IEEE ยอมรับได้ที่ 5%)
บทความนี้เกิดจากการเขียนและส่งขึ้นมาสู่ระบบแบบอัตโนมัติ สมาคมฯไม่รับผิดชอบต่อบทความหรือข้อความใดๆ ทั้งสิ้น เพราะไม่สามารถระบุได้ว่าเป็นความจริงหรือไม่ ผู้อ่านจึงควรใช้วิจารณญาณในการกลั่นกรอง และหากท่านพบเห็นข้อความใดที่ขัดต่อกฎหมายและศีลธรรม หรือทำให้เกิดความเสียหาย หรือละเมิดสิทธิใดๆ กรุณาแจ้งมาที่ ht.ro.apt@ecivres-bew เพื่อทีมงานจะได้ดำเนินการลบออกจากระบบในทันที