“คุณใช้ชิ้นงาน 10 ชิ้น โดยใช้พนักงานวัด 3 คน และทำการวัดซ้ำ 2 ครั้ง”
แนวความคิดพื้นฐานของการทำการทดสอบเครื่องมือวัด (Gage R&R) เป็นหลักการที่คนโดยทั่วไปยอมรับและมีคำถามน้อยมากว่ามันมีประสิทธิภาพหรือไม่ ในคำถามอาจจะเป็นการมองว่าใช้พนักงานวัด 3 คน หรือ จำนวนซ้ำ 2 นั้นเพียงพอหรือไม่ ในบทความเรื่อง “ การวัดเครื่องมือวัด โดยใช้ชิ้นงาน 10 ชิ้น” (“Gauging Gage” I want to look at 10) คุณจะประเมินระบบการวัดของคุณได้อย่างไรด้วยการใช้ชิ้นงาน 10 ชิ้น
การประเมินระบบการวัดด้วยชิ้นงาน 10 ชิ้น
ผมจะยกกรณีง่ายๆเป็นตัวอย่างประกอบการอธิบาย โดยเริ่มทำการจำลองข้อมูลด้วยการทดลองของ Gage R&R จำนวน 1000 ครั้ง ซึ่งได้ผลลัพธ์ของการทดลองเป็นดังนี้
1 : ไม่มีความแตกต่างระหว่างพนักงานวัด และ ไม่มี interaction ระหว่าง ชิ้นงานและพนักงานวัด
2 : ความผันแปรของระบบการวัด และ ความผันแปรระหว่างชิ้นงานมี % contribution คือ 5.85% โดยมีคำแนะนำทั่วไปไว้ว่า ถ้า <1% จะถือว่ามีระบบดีเลิศ และ ถ้า >9% จะถือว่ามีระบบที่ไม่ดี
ดังนั้น จากการจำลองสถานการณ์ของการทดลองจำนวน 1000 ครั้ง คุณคิดว่าค่า % Contribution จะมีการแจกแจงเป็นแบบไหน โดยเฉพาะค่ากลางนั้นใกล้กับค่าจริง (5.85%) แค่ไหน หรือ การแจกแจงนั้นมีความเบ้หรือไม่ และถ้ามีค่าประมาณที่หาได้จะมีความผันแปรมากเท่าไหร่
ใช้เวลาลองคิดหาคำตอบสักพัก............
ตกลง.... พร้อมฟังคำตอบ
จากภาพข้างล่าง คือ การแจกแจงและเทียบเคียงกับค่าที่แนะนำไว้ รวมทั้งค่าจริง ซึ่งแสดงให้เห็นในกราฟ
ข่าวดี คือ จะเห็นว่าค่ากลาง (ค่าเฉลี่ย) ใกล้เคียงค่าจริง
อย่างไรก็ตามการแจกแจงมีความเบ้มาก จำนวนข้อมูลที่เหมาะสม ที่ใช้ประมาณค่า % Contribution ได้อย่างน้อยเป็น 2 เท่าของค่าจริง และ มีค่าประมาณหนึ่งค่าที่มีค่า 6 เท่าของค่าจริง จะเห็นว่าความผันแปรมีขนาดใหญ่มาก ในความเป็นจริง จากการศึกษา 1 ใน 4 ครั้งจะแสดงว่าเครื่องมือวัดนี้ใช้ไม่ได้
ตอนนี้การศึกษาเครื่องมือวัดไม่ใช่งานเล็กๆ จะต้องมีการเก็บข้อมูล จำนวนข้อมูล 60 ข้อมูล โดยทำภายใต้หลักการ randomization และ ทำกำหนดวัดตำแหน่งบนชื้นงานเพื่อทำการวัด ซึ่งจำนวนชิ้นงานยิ่งเยอะ ยิ่งทำให้เกิดความเบื่อหน่ายสำหรับคนงาน ดังนั้นเราจึงต้องทำการหาว่าจำนวนชิ้นงานเท่าไหร่ที่จะถูกนำมาใช้ในงานเพื่อจะนำมาใช้ในการประเมินค่า %Contribution ได้อย่างถูกต้อง
การประเมินระบบการวัดด้วยชิ้นงานจำนวน 30 ชิ้น
ผมทำการจำลองสถานการณ์จำนวน 1000 ครั้ง แต่ละครั้งจะใช้ชิ้นงาน 30 ชื้น (เท่ากับว่าแต่ละครั้งมีข้อมูล 180 ข้อมูล/จุด) และทำอีกครั้งโดยใช้ชิ้นงานจำนวน 100 ชิ้น (เท่ากับข้อมูล 600 จุด) และทำการพิจารณาสิ่งต่อไปนี้ คือ ค่าเฉลี่ย ความเบ้ และ ความผันแปร
ค่าเฉลี่ย อาจจะไม่ยาก เพราะถ้ามันอยู่ตรงกลางมาก่อน มันก็ควรจะยังอยู่ตรงกลางเหมือนเดิม
ดังนั้นมาดูเรื่อง ความเบ้ และดูว่าเราจะลดความผันแปรได้เท่าไหร่
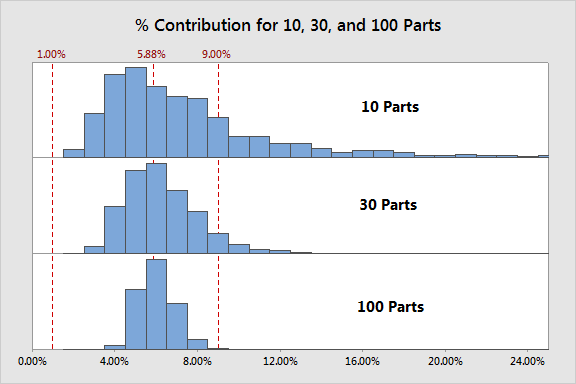
ความเบ้และความผันแปร นั้นมีค่าลดลงอย่างชัดเจน แต่ผมสงสัยว่าคุณกำลังคิดว่าความผันแปรนั้นลดลงมากกว่าที่ควรจะเป็นหรือไม่ เนื่องจาก %Contribution มีอิทธิพลจากค่าประมาณของ repeatability และ reproducibility คุณอาจจะทำการบีบให้การแจกแจงแคบลงด้วยการเพิ่มจำนวนชิ้นงาน แต่จำนวนงานที่จะต้องทำจะมีมากกขึ้นด้วย แค่เพียงชิ้นงาน 30 ชิ้น จำนวนการทดลองที่ต้องทำก็มีมากมาย แต่ผลลัพธ์ของเครื่องมือวัดยังคงเป็น 7%
แล้วเราควรทำอะไรต่อ
มีข้อแนะนำอยู่ 2 ข้อ
ข้อแนะนำที่ 1 พิจารณา %Process หลายครั้งเราประเมินระบบการวัด เพื่อดูว่ามีประสิทธิภาพหรือไม่ ในกรณีนี้แทนที่จะใช้สิ่งตัวอย่างจำนวนน้อยเพื่อประมาณค่าความผันแปรทั้งหมด คุณอาจจะใช้ค่าเบี่ยงเบนมาตรฐานในอดีตเป็นค่าประมาณแทน เพื่อกำจัดความผันแปรที่เกิดจากจำนวนสิ่งตัวอย่างของชิ้นงานที่ต้องใช้ ด้วยการเปิด Subdialog ใน Minitab เพื่อใส่ค่า Historical standard deviation
ในการทำแบบนี้ ผลลัพธ์ในการคำนวณจะเพิ่มอีก 1 คอลัมน์เรียกว่า %Process ซึ่งมีความเท่าเทียมกับ %StudyVar เพียงแต่ใช้ค่าเบี่ยงเบนมาตรฐานในอดีต (ซึ่งมาจากสิ่งตัวอย่างที่มีขนาดใหญ่) แทนที่จะใช้ค่า เบี่ยงเบนมาตรฐาน overall ของข้อมูลที่มาจากการทดลอง
ส่วนข้อแนะนำที่ 2 คือ ให้พิจารณาช่วงความเชื่อมั่นของผลลัพธ์ร่วมด้วย ซึ่งสามารถทำได้ด้วยการเลือกใน Conf Int ของ subdialog
แม้ว่าผลของช่วงความเชื่อมั่นจะไม่ได้ช่วยเรื่องการปรับปรุงความผันแปรของเครื่องมือวัด แต่ค่าประมาณนี้จะช่วยทำให้รู้ได้ว่าค่าประมาณนั้นมีความไม่แน่นอนเท่าไหร่ เช่น จากตัวอย่างที่ได้จาก gageiag.mtw ที่เป็นชุดข้อมูลตัวอย่างของ Minitab เกี่ยวกับเรื่องช่วงความเชื่อมั่นแสดงให้เห็นดังนี้
สำหรับบางกระบวนการ เครื่องมือวัดอาจเป็นที่ยอมรับได้เมื่อ %Contribution นั้นน้อยกว่า 9% แต่บางกระบวนการที่สำคัญ อาจจะต้องมีการพิจารณาบางอย่างเพิ่ม จาก 95% ช่วงความเชื่อมั่นที่มีค่า (2.14, 66.18) เป็นเหมือนสัญญาณเตือนว่าเครื่องมือวัดนี้ไม่ควรจะได้รับการยอมรับ
ในการศึกษาเครื่องมือวัดครั้งต่อไป คุณควรสนใจด้วยว่าจะต้องใช้ชิ้นงานจำนวนกี่ชิ้น และผลลัพธ์ที่ได้นั้นมีความเชื่อถือได้เท่าไหร่
บทความต้นฉบับ : http://blog.minitab.com/blog/fun-with-statistics/gauging-gage-part-1-is-10-parts-enough
เนื้อหาบทความโดยบริษัท Minitab Inc. ประเทศสหรัฐอเมริกา
แปลและเรียบเรียงโดยสุวดี นําพาเจริญ และ ชลทิขา จํารัสพร, บริษัท โซลูชั่น เซ็นเตอร์ จํากัด webadmin@solutioncenterminitab.com
บทความนี้เกิดจากการเขียนและส่งขึ้นมาสู่ระบบแบบอัตโนมัติ สมาคมฯไม่รับผิดชอบต่อบทความหรือข้อความใดๆ ทั้งสิ้น เพราะไม่สามารถระบุได้ว่าเป็นความจริงหรือไม่ ผู้อ่านจึงควรใช้วิจารณญาณในการกลั่นกรอง และหากท่านพบเห็นข้อความใดที่ขัดต่อกฎหมายและศีลธรรม หรือทำให้เกิดความเสียหาย หรือละเมิดสิทธิใดๆ กรุณาแจ้งมาที่ ht.ro.apt@ecivres-bew เพื่อทีมงานจะได้ดำเนินการลบออกจากระบบในทันที