ในบทความส่วนที่ 1 และ 2 ได้พูดถึงเรื่องจำนวนชิ้นงานวัด จำนวนพนักงานวัด และ จำนวนการวัดซ้ำ ที่ใช้ในการทดสอบเครื่องมือวัด (R&R study) และประมาณค่า % Contribution ในแต่ละสถานการณ์ไปแล้ว ในการทดลองที่ทำนั้นได้พบสิ่งที่น่าสนใจอย่างมาก โดยเฉพาะสิ่งที่บทความนั้นได้ชี้ถึงข้อผิดพลาดที่ผมเคยทำในการทดสอบและหวังว่ามันจะไม่ทำให้คุณเป็นแบบผม
เราจะเริ่มจาก พนักงานวัด โดยจะใช้เครื่องมือแบบเดียวกับในบทความส่วนที่ 1 ในการจำลองสถานการณ์ และครั้งนี้จะทำการจำลองสถานการณ์ 2 แบบที่แตกต่างกัน คือ เพิ่มพนักงานวัดเป็น 4 คน แต่ยังใช้จำนวนชิ้นงาน 10 ชิ้น และทำซ้ำ 2 ครั้ง (ซึ่งเท่ากับจำนวนข้อมูลทั้งหมดที่จะได้คือ 80 ข้อมูล) อีกหนึ่งสถานการณ์ คือ เพิ่มจำนวนพนักงานวัดเป็น 4 คน และใช้จำนวนซ้ำ 2 ครั้ง แต่ลดจำนวนชิ้นงานลงเป็น 8 ชิ้น ซึ่งทำให้จำนวนการทำการทดลองทั้งหมดลดลงใกล้เคียงกับที่เริ่มต้น (ของใหม่คือ64 ข้อมูล ซึ่งใกล้เคียงกับของเดิมคือ 60 ข้อมูล ซึ่งเป็นการทดลองเริ่มต้น)
และการเปรียบเทียบการทดลองแบบต่างๆตามกราฟ
ในส่วนที่ 3 นี้ ผมจะพูดถึงสิ่งที่ทำให้ผมปวดหัวและกวนใจผมได้ตลอด และผมพบเรื่องแบบนี้เสมอ และคุณเองก็อาจจะทำเรื่องแบบนี้ด้วยเช่นกัน ถ้าคุณทำเช่นนี้ ผมกำลังจะบอกว่าคุณกำลังทำสิ่งที่ผิดอยู่ ถ้าคุณเป็นผู้สอน คุณอาจจะต้องติดต่อนักเรียนของคุณเพื่อกล่าวคำขอโทษและยอมรับว่าคุณได้แนะนำสิ่งผิดไป และนั้นเป็นการสมมติแบบด้านบวก หรือคุณอาจจะทิ้งข้อความเพื่อค้านผมว่าผมผิดและต่อว่ากับหลักฐานต่างๆที่ผมได้มีให้ว่าผมคิดถูก
ขอผมถามคำถามคุณหนึ่งข้อ
ในตอนที่คุณศึกษาเรื่อง Gage R&R คุณเลือกชิ้นงานที่จะทำการวัดอย่างไร
ถ้าคำตอบของคุณเป็นเพียงคำตอบสั้นๆ ซึ่งโดยทั่วไปก็เป็นเช่นนั้น แต่ผมกลัวว่ามันจะไม่ใช่คำตอบที่ถูกต้องนัก ถ้าคุณกำลังเป็นแบบนั้น ผมเดาว่าคุณกำลังคิดว่ามีความคิดขัดแย้งอยู่ และถึงแม้ผมจะไม่ได้ยินที่คุณคิดแต่ผมคงต้องบอกว่าคุณมีข้อโต้แย้งกับสิ่งที่ผมบอกนั้น ใช่ไหมครับ ลองดูว่าคำตอบของคุณเป็นแบบที่ผมยกตัวอย่างหรือไม่
- ชิ้นงานตัวอย่างที่เลือกมาอยู่ในช่วงย่านการวัดที่ใช้งานอยู่
- ชิ้นงานตัวอย่างที่เลือกมาอยู่ในช่วงค่าเผื่อของกระบวนการ (Process tolerance) ในขอบเขตข้อกำหนดเฉพาะด้านล่างและด้านบน
- ชิ้นงานตัวอย่างถูกเลือกมาอย่างสุ่มจากส่วนนอกที่อยู่ขอบเขตข้อจำกัดเฉพาะทั้งสองด้าน
คำตอบทั้ง 3 ข้อ ผิด
คุณจะเห็นว่าสถิติที่คุณใช้ในการประเมินระบบการวัดของคุณ จะหาค่าที่เกี่ยวข้องกับความผันแปรแบบ part-to-part และรูปแบบการเลือกชิ้นงานทั้งสามแบบนั้นไม่สามารถประมาณค่าความผันแปร part-to-part ได้อย่างถูกต้อง คำตอบสำหรับคำถามนี้จะต้องให้วิธีการที่จะประมาณค่าได้อย่างสมเหตุสมผล
“อย่างสุม” (Randomly)
ผมว่าเราควรจะเข้าเรื่องกันได้แล้ว เนื่องจากบทความนี้เป็นเรื่องเกี่ยวกับสถิติ เราจะพูดแบบสถิติเล็กน้อย
ในบทความส่วนที่ 1 เราได้จำลองการทดลองของ Gage R&R โดยทำการใช้ชิ้นงานวัด 10 ชิ้น พนักงานวัด 3 คน และทำการวัดซ้ำ 2 ครั้ง โดยทำการจำลองการทดลองทั้งหมด 1000 ครั้ง และจะให้การทดลองนี้เป็นบรรทัดฐาน จากนั้นผมจะทำการจำลองการทดลองด้วยรูปแบบอื่นดังต่อไปนี้
- การสุ่มตัวอย่างแบบ “exact” ซึ่งในชีวิตจริงไม่สามารถทำได้ โดยจะทำการเลือกชิ้นงานตามลำดับเปอร์เซนไทล์ที่ 5, 15 ,25,….,จนถึง ที่ 95 ซึ่งมีการแจกแจงใกล้เคียงการแจกแจงแบบปกติ (Normal distribution) และเมื่อการแจกแจงใกล้เคียง “exact” แบบปกติ (normal distribution) ซึ่งจะทำให้เราได้เห็นว่าการเลือกตัวอย่างแบบสุ่มนั้นมีผลต่อการประมาณค่าอย่างไร
- ชิ้นงานจะถูกเลือกจากกระบวนการผลิตที่ช่วงเวลาผลิตนั้นถูกแบ่งอย่างเท่าๆกัน (Uniformly) โดยเลือกจากช่วงเปอร์เซนต์ไทล์ระหว่างที่ 5 ถึง 95
- ชิ้นงานจะถูกเลือกจากช่วงของข้อกำหนดเฉพาะที่แบ่งไว้อย่างเท่าๆกัน ในกรณีนี้สมมติว่ากระบวนการนั้นมีค่ากลางที่ไม่เปลี่ยนแปลง (shift) ด้วยค่า Ppk เท่ากับ 1
- ชิ้นงาน 8 ชิ้นจาก 10 ชิ้น ถูกเลือกอย่างสุ่ม และอีก 2 ชิ้นที่เหลือจะเลือกจากชิ้นงานที่อยู่ในช่วงของ ครึ่งหนึ่งของค่าเบี่ยงเบนมาตรฐานที่อยู่นอกเขตกำหนดเฉพาะ(ทั้งซ้ายและขวา)
โดยมีค่า % Contribution ที่รู้แน่นอนว่าคือ 5.88325% (ซึ่งเราใช้เป็นบรรทัดฐาน)
เลือกชิ้นงานอย่างสุ่มเพื่อการวัด (Randomly Sampling for Gage)
เราใช้พจน์ “random” เพื่อเป็นมาตรฐานในการเปรียบเทียบกับสิ่งที่เราทำไว้ในบทความส่วนที่ 1 และ 2 ซึ่งไม่ได้ให้ค่าประมาณที่ถูกต้องนัก
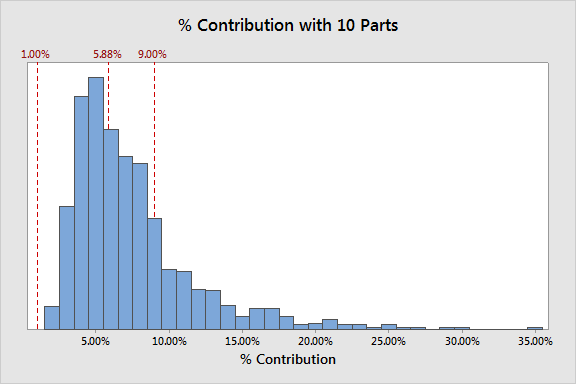
ในหลายๆครั้ง ที่คนทำการทดลองมักจะบอกผมว่า ไม่สามารถทำการสุ่มได้เพราะว่าชิ้นงานที่ได้มานั้นไม่ได้มีการแจกแจงแบบที่ควรจะเป็น
ชิ้นงานตัวอย่าง 10 ชิ้น มีการแจกแจงแบบที่ตั้งไว้หรือไม่
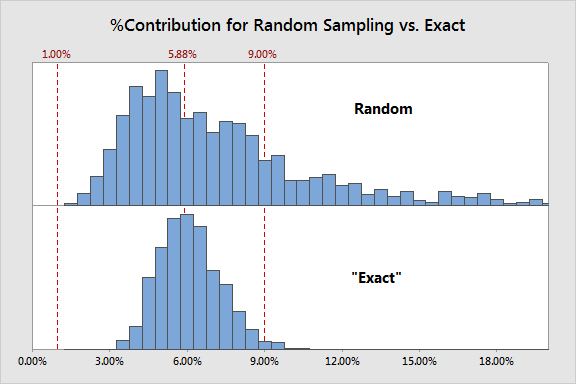
มาเปรียบเทียบสถานการณ์การเลือกชิ้นงานแบบ random กับ แบบ exact โดยถ้าเรามีพลังวิเศษทำการเลือกชิ้นงานมาได้ 10 ชิ้น เราจะได้การแจกแจงของชิ้นงานที่เกือบสมบูรณ์แบบ หมายความว่าเราได้กำจัดทิ้งผลกระทบของการสุ่ม (randomness) ออกไป
เครื่องมือวัด ส่วนที่ 3: การสุ่มตัวอย่างชิ้นงานวัด (Gauging Gage Part 3: How to Sample Parts)
ในบทความส่วนที่ 1 และ 2 ได้พูดถึงเรื่องจำนวนชิ้นงานวัด จำนวนพนักงานวัด และ จำนวนการวัดซ้ำ ที่ใช้ในการทดสอบเครื่องมือวัด (R&R study) และประมาณค่า % Contribution ในแต่ละสถานการณ์ไปแล้ว ในการทดลองที่ทำนั้นได้พบสิ่งที่น่าสนใจอย่างมาก โดยเฉพาะสิ่งที่บทความนั้นได้ชี้ถึงข้อผิดพลาดที่ผมเคยทำในการทดสอบและหวังว่ามันจะไม่ทำให้คุณเป็นแบบผม
เราจะเริ่มจาก พนักงานวัด โดยจะใช้เครื่องมือแบบเดียวกับในบทความส่วนที่ 1 ในการจำลองสถานการณ์ และครั้งนี้จะทำการจำลองสถานการณ์ 2 แบบที่แตกต่างกัน คือ เพิ่มพนักงานวัดเป็น 4 คน แต่ยังใช้จำนวนชิ้นงาน 10 ชิ้น และทำซ้ำ 2 ครั้ง (ซึ่งเท่ากับจำนวนข้อมูลทั้งหมดที่จะได้คือ 80 ข้อมูล) อีกหนึ่งสถานการณ์ คือ เพิ่มจำนวนพนักงานวัดเป็น 4 คน และใช้จำนวนซ้ำ 2 ครั้ง แต่ลดจำนวนชิ้นงานลงเป็น 8 ชิ้น ซึ่งทำให้จำนวนการทำการทดลองทั้งหมดลดลงใกล้เคียงกับที่เริ่มต้น (ของใหม่คือ64 ข้อมูล ซึ่งใกล้เคียงกับของเดิมคือ 60 ข้อมูล ซึ่งเป็นการทดลองเริ่มต้น)
และการเปรียบเทียบการทดลองแบบต่างๆตามกราฟ
ในส่วนที่ 3 นี้ ผมจะพูดถึงสิ่งที่ทำให้ผมปวดหัวและกวนใจผมได้ตลอด และผมพบเรื่องแบบนี้เสมอ และคุณเองก็อาจจะทำเรื่องแบบนี้ด้วยเช่นกัน ถ้าคุณทำเช่นนี้ ผมกำลังจะบอกว่าคุณกำลังทำสิ่งที่ผิดอยู่ ถ้าคุณเป็นผู้สอน คุณอาจจะต้องติดต่อนักเรียนของคุณเพื่อกล่าวคำขอโทษและยอมรับว่าคุณได้แนะนำสิ่งผิดไป และนั้นเป็นการสมมติแบบด้านบวก หรือคุณอาจจะทิ้งข้อความเพื่อค้านผมว่าผมผิดและต่อว่ากับหลักฐานต่างๆที่ผมได้มีให้ว่าผมคิดถูก
ขอผมถามคำถามคุณหนึ่งข้อ
ในตอนที่คุณศึกษาเรื่อง Gage R&R คุณเลือกชิ้นงานที่จะทำการวัดอย่างไร
ถ้าคำตอบของคุณเป็นเพียงคำตอบสั้นๆ ซึ่งโดยทั่วไปก็เป็นเช่นนั้น แต่ผมกลัวว่ามันจะไม่ใช่คำตอบที่ถูกต้องนัก ถ้าคุณกำลังเป็นแบบนั้น ผมเดาว่าคุณกำลังคิดว่ามีความคิดขัดแย้งอยู่ และถึงแม้ผมจะไม่ได้ยินที่คุณคิดแต่ผมคงต้องบอกว่าคุณมีข้อโต้แย้งกับสิ่งที่ผมบอกนั้น ใช่ไหมครับ ลองดูว่าคำตอบของคุณเป็นแบบที่ผมยกตัวอย่างหรือไม่
- ชิ้นงานตัวอย่างที่เลือกมาอยู่ในช่วงย่านการวัดที่ใช้งานอยู่
- ชิ้นงานตัวอย่างที่เลือกมาอยู่ในช่วงค่าเผื่อของกระบวนการ (Process tolerance) ในขอบเขตข้อกำหนดเฉพาะด้านล่างและด้านบน
- ชิ้นงานตัวอย่างถูกเลือกมาอย่างสุ่มจากส่วนนอกที่อยู่ขอบเขตข้อจำกัดเฉพาะทั้งสองด้าน
คำตอบทั้ง 3 ข้อ ผิด
คุณจะเห็นว่าสถิติที่คุณใช้ในการประเมินระบบการวัดของคุณ จะหาค่าที่เกี่ยวข้องกับความผันแปรแบบ part-to-part และรูปแบบการเลือกชิ้นงานทั้งสามแบบนั้นไม่สามารถประมาณค่าความผันแปร part-to-part ได้อย่างถูกต้อง คำตอบสำหรับคำถามนี้จะต้องให้วิธีการที่จะประมาณค่าได้อย่างสมเหตุสมผล
“อย่างสุม” (Randomly)
ผมว่าเราควรจะเข้าเรื่องกันได้แล้ว เนื่องจากบทความนี้เป็นเรื่องเกี่ยวกับสถิติ เราจะพูดแบบสถิติเล็กน้อย
ในบทความส่วนที่ 1 เราได้จำลองการทดลองของ Gage R&R โดยทำการใช้ชิ้นงานวัด 10 ชิ้น พนักงานวัด 3 คน และทำการวัดซ้ำ 2 ครั้ง โดยทำการจำลองการทดลองทั้งหมด 1000 ครั้ง และจะให้การทดลองนี้เป็นบรรทัดฐาน จากนั้นผมจะทำการจำลองการทดลองด้วยรูปแบบอื่นดังต่อไปนี้
- การสุ่มตัวอย่างแบบ “exact” ซึ่งในชีวิตจริงไม่สามารถทำได้ โดยจะทำการเลือกชิ้นงานตามลำดับเปอร์เซนไทล์ที่ 5, 15 ,25,….,จนถึง ที่ 95 ซึ่งมีการแจกแจงใกล้เคียงการแจกแจงแบบปกติ (Normal distribution) และเมื่อการแจกแจงใกล้เคียง “exact” แบบปกติ (normal distribution) ซึ่งจะทำให้เราได้เห็นว่าการเลือกตัวอย่างแบบสุ่มนั้นมีผลต่อการประมาณค่าอย่างไร
- ชิ้นงานจะถูกเลือกจากกระบวนการผลิตที่ช่วงเวลาผลิตนั้นถูกแบ่งอย่างเท่าๆกัน (Uniformly) โดยเลือกจากช่วงเปอร์เซนต์ไทล์ระหว่างที่ 5 ถึง 95
- ชิ้นงานจะถูกเลือกจากช่วงของข้อกำหนดเฉพาะที่แบ่งไว้อย่างเท่าๆกัน ในกรณีนี้สมมติว่ากระบวนการนั้นมีค่ากลางที่ไม่เปลี่ยนแปลง (shift) ด้วยค่า Ppk เท่ากับ 1
- ชิ้นงาน 8 ชิ้นจาก 10 ชิ้น ถูกเลือกอย่างสุ่ม และอีก 2 ชิ้นที่เหลือจะเลือกจากชิ้นงานที่อยู่ในช่วงของ ครึ่งหนึ่งของค่าเบี่ยงเบนมาตรฐานที่อยู่นอกเขตกำหนดเฉพาะ(ทั้งซ้ายและขวา)
โดยมีค่า % Contribution ที่รู้แน่นอนว่าคือ 5.88325% (ซึ่งเราใช้เป็นบรรทัดฐาน)
เลือกชิ้นงานอย่างสุ่มเพื่อการวัด (Randomly Sampling for Gage)
เราใช้พจน์ “random” เพื่อเป็นมาตรฐานในการเปรียบเทียบกับสิ่งที่เราทำไว้ในบทความส่วนที่ 1 และ 2 ซึ่งไม่ได้ให้ค่าประมาณที่ถูกต้องนัก

ในหลายๆครั้ง ที่คนทำการทดลองมักจะบอกผมว่า ไม่สามารถทำการสุ่มได้เพราะว่าชิ้นงานที่ได้มานั้นไม่ได้มีการแจกแจงแบบที่ควรจะเป็น
ชิ้นงานตัวอย่าง 10 ชิ้น มีการแจกแจงแบบที่ตั้งไว้หรือไม่
มาเปรียบเทียบสถานการณ์การเลือกชิ้นงานแบบ random กับ แบบ exact โดยถ้าเรามีพลังวิเศษทำการเลือกชิ้นงานมาได้ 10 ชิ้น เราจะได้การแจกแจงของชิ้นงานที่เกือบสมบูรณ์แบบ หมายความว่าเราได้กำจัดทิ้งผลกระทบของการสุ่ม (randomness) ออกไป

จะเห็นว่ามีบางอย่างที่แสดงไว้ชัดเจนเกี่ยวกับเรื่องการสุ่ม ที่มาจากการสุ่มตัวอย่าง (random sampling) ซึ่งมีผลกระทบมากต่อการประมาณค่า %Contribution โดยการการแจกแจงของรูปแบบการทดลองแบบ exact จะเห็นว่ามีการเบ้ (Skew) และความผันแปรน้อยกว่า ซึ่งทำให้การประเมินระบบการวัดทำได้ดีขึ้น ในการทำการทดลองแบบ exact นั้นไม่สามารถทำได้จริงในเกือบทุกๆกรณี เพราะว่าคุณไม่รู้ว่าระบบของคุณมีความคลาดเคลื่อน (error)เท่าไหร่ และนั้นทำให้ไม่สามารถทำให้เกิดการแจกแจงที่ถูกต้องได้ ซึ่งเป็นปัญหาโลกแตกเหมือนหาว่าไก่กับไข่อะไรเกิดก่อนกัน
สุ่มแบบ Uniform จากค่าช่วงของค่าชิ้นงานที่เป็นอยู่
มาต่อที่รูปแบบการสุ่มแบบที่ 2 เราจะทำการเปรียบเทียบ ได้ผลดังนี้
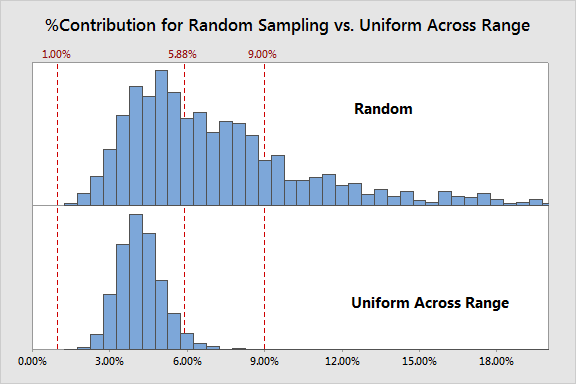
เราได้ผลแบบใหม่ จะเห็นได้ว่าความผันแปรลดลงแต่มี bias อย่างชัดเจน ในการทำแบบนี้เราจะดึงชิ้นงานแบบ uniform ตลอดช่วงของชิ้นงานซึ่งจะทำให้การประมาณค่านั้นมีความเสถียร(consistent) ขึ้น ทำให้ค่าประมาณที่ได้บ่งบอกว่าระบบการวัดนั้นดีมากกว่าที่ระบบนั้นเป็นจริง
สุ่มแบบ uniform ตลอดช่วงข้อกำหนดเฉพาะ
ผลที่ได้เป็นดังนี้
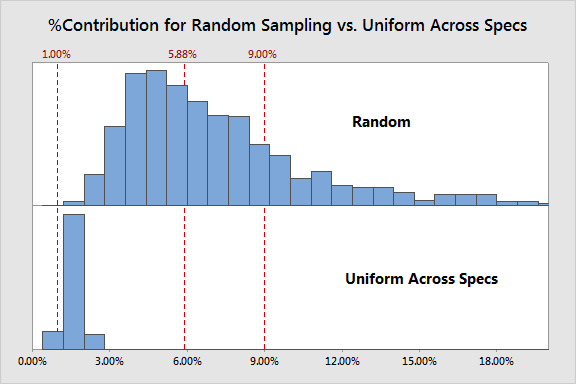
รูปแบบการสุ่มแบบนี้จะเห็นว่ามีค่า bias อย่างมาก ซึ่งทำให้การประเมินระบบการวัดที่ได้เป็น excellence คงไม่จำเป็นต้องบอกว่า ผลการประเมินนี้ไม่มีความถูกต้องเลย
การสุ่มชิ้นงานจากช่วงที่อยู่นอกข้อกำหนดเฉพาะ
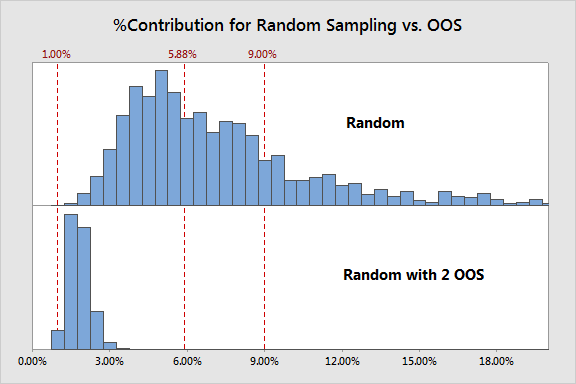
รูปแบบสุดท้าย คือ เลือกชิ้นงานแบบสุ่ม และมีหนึ่งชิ้นที่เลือกจากช่วงที่อยู่นอกขอบเขตกำหนดเฉพาะ หมายความว่าจะมีจุดข้อมูล 2 จุด ออกนอกเขตกำหนดเฉพาะ จะมีผลแตกต่างอย่างชัดเจน แบบนั้นหรือไม่
เครื่องมือวัด ส่วนที่ 3: การสุ่มตัวอย่างชิ้นงานวัด (Gauging Gage Part 3: How to Sample Parts)
ในบทความส่วนที่ 1 และ 2 ได้พูดถึงเรื่องจำนวนชิ้นงานวัด จำนวนพนักงานวัด และ จำนวนการวัดซ้ำ ที่ใช้ในการทดสอบเครื่องมือวัด (R&R study) และประมาณค่า % Contribution ในแต่ละสถานการณ์ไปแล้ว ในการทดลองที่ทำนั้นได้พบสิ่งที่น่าสนใจอย่างมาก โดยเฉพาะสิ่งที่บทความนั้นได้ชี้ถึงข้อผิดพลาดที่ผมเคยทำในการทดสอบและหวังว่ามันจะไม่ทำให้คุณเป็นแบบผม
เราจะเริ่มจาก พนักงานวัด โดยจะใช้เครื่องมือแบบเดียวกับในบทความส่วนที่ 1 ในการจำลองสถานการณ์ และครั้งนี้จะทำการจำลองสถานการณ์ 2 แบบที่แตกต่างกัน คือ เพิ่มพนักงานวัดเป็น 4 คน แต่ยังใช้จำนวนชิ้นงาน 10 ชิ้น และทำซ้ำ 2 ครั้ง (ซึ่งเท่ากับจำนวนข้อมูลทั้งหมดที่จะได้คือ 80 ข้อมูล) อีกหนึ่งสถานการณ์ คือ เพิ่มจำนวนพนักงานวัดเป็น 4 คน และใช้จำนวนซ้ำ 2 ครั้ง แต่ลดจำนวนชิ้นงานลงเป็น 8 ชิ้น ซึ่งทำให้จำนวนการทำการทดลองทั้งหมดลดลงใกล้เคียงกับที่เริ่มต้น (ของใหม่คือ64 ข้อมูล ซึ่งใกล้เคียงกับของเดิมคือ 60 ข้อมูล ซึ่งเป็นการทดลองเริ่มต้น)
และการเปรียบเทียบการทดลองแบบต่างๆตามกราฟ
ในส่วนที่ 3 นี้ ผมจะพูดถึงสิ่งที่ทำให้ผมปวดหัวและกวนใจผมได้ตลอด และผมพบเรื่องแบบนี้เสมอ และคุณเองก็อาจจะทำเรื่องแบบนี้ด้วยเช่นกัน ถ้าคุณทำเช่นนี้ ผมกำลังจะบอกว่าคุณกำลังทำสิ่งที่ผิดอยู่ ถ้าคุณเป็นผู้สอน คุณอาจจะต้องติดต่อนักเรียนของคุณเพื่อกล่าวคำขอโทษและยอมรับว่าคุณได้แนะนำสิ่งผิดไป และนั้นเป็นการสมมติแบบด้านบวก หรือคุณอาจจะทิ้งข้อความเพื่อค้านผมว่าผมผิดและต่อว่ากับหลักฐานต่างๆที่ผมได้มีให้ว่าผมคิดถูก
ขอผมถามคำถามคุณหนึ่งข้อ
ในตอนที่คุณศึกษาเรื่อง Gage R&R คุณเลือกชิ้นงานที่จะทำการวัดอย่างไร
ถ้าคำตอบของคุณเป็นเพียงคำตอบสั้นๆ ซึ่งโดยทั่วไปก็เป็นเช่นนั้น แต่ผมกลัวว่ามันจะไม่ใช่คำตอบที่ถูกต้องนัก ถ้าคุณกำลังเป็นแบบนั้น ผมเดาว่าคุณกำลังคิดว่ามีความคิดขัดแย้งอยู่ และถึงแม้ผมจะไม่ได้ยินที่คุณคิดแต่ผมคงต้องบอกว่าคุณมีข้อโต้แย้งกับสิ่งที่ผมบอกนั้น ใช่ไหมครับ ลองดูว่าคำตอบของคุณเป็นแบบที่ผมยกตัวอย่างหรือไม่
- ชิ้นงานตัวอย่างที่เลือกมาอยู่ในช่วงย่านการวัดที่ใช้งานอยู่
- ชิ้นงานตัวอย่างที่เลือกมาอยู่ในช่วงค่าเผื่อของกระบวนการ (Process tolerance) ในขอบเขตข้อกำหนดเฉพาะด้านล่างและด้านบน
- ชิ้นงานตัวอย่างถูกเลือกมาอย่างสุ่มจากส่วนนอกที่อยู่ขอบเขตข้อจำกัดเฉพาะทั้งสองด้าน
คำตอบทั้ง 3 ข้อ ผิด
คุณจะเห็นว่าสถิติที่คุณใช้ในการประเมินระบบการวัดของคุณ จะหาค่าที่เกี่ยวข้องกับความผันแปรแบบ part-to-part และรูปแบบการเลือกชิ้นงานทั้งสามแบบนั้นไม่สามารถประมาณค่าความผันแปร part-to-part ได้อย่างถูกต้อง คำตอบสำหรับคำถามนี้จะต้องให้วิธีการที่จะประมาณค่าได้อย่างสมเหตุสมผล
“อย่างสุม” (Randomly)
ผมว่าเราควรจะเข้าเรื่องกันได้แล้ว เนื่องจากบทความนี้เป็นเรื่องเกี่ยวกับสถิติ เราจะพูดแบบสถิติเล็กน้อย
ในบทความส่วนที่ 1 เราได้จำลองการทดลองของ Gage R&R โดยทำการใช้ชิ้นงานวัด 10 ชิ้น พนักงานวัด 3 คน และทำการวัดซ้ำ 2 ครั้ง โดยทำการจำลองการทดลองทั้งหมด 1000 ครั้ง และจะให้การทดลองนี้เป็นบรรทัดฐาน จากนั้นผมจะทำการจำลองการทดลองด้วยรูปแบบอื่นดังต่อไปนี้
- การสุ่มตัวอย่างแบบ “exact” ซึ่งในชีวิตจริงไม่สามารถทำได้ โดยจะทำการเลือกชิ้นงานตามลำดับเปอร์เซนไทล์ที่ 5, 15 ,25,….,จนถึง ที่ 95 ซึ่งมีการแจกแจงใกล้เคียงการแจกแจงแบบปกติ (Normal distribution) และเมื่อการแจกแจงใกล้เคียง “exact” แบบปกติ (normal distribution) ซึ่งจะทำให้เราได้เห็นว่าการเลือกตัวอย่างแบบสุ่มนั้นมีผลต่อการประมาณค่าอย่างไร
- ชิ้นงานจะถูกเลือกจากกระบวนการผลิตที่ช่วงเวลาผลิตนั้นถูกแบ่งอย่างเท่าๆกัน (Uniformly) โดยเลือกจากช่วงเปอร์เซนต์ไทล์ระหว่างที่ 5 ถึง 95
- ชิ้นงานจะถูกเลือกจากช่วงของข้อกำหนดเฉพาะที่แบ่งไว้อย่างเท่าๆกัน ในกรณีนี้สมมติว่ากระบวนการนั้นมีค่ากลางที่ไม่เปลี่ยนแปลง (shift) ด้วยค่า Ppk เท่ากับ 1
- ชิ้นงาน 8 ชิ้นจาก 10 ชิ้น ถูกเลือกอย่างสุ่ม และอีก 2 ชิ้นที่เหลือจะเลือกจากชิ้นงานที่อยู่ในช่วงของ ครึ่งหนึ่งของค่าเบี่ยงเบนมาตรฐานที่อยู่นอกเขตกำหนดเฉพาะ(ทั้งซ้ายและขวา)
โดยมีค่า % Contribution ที่รู้แน่นอนว่าคือ 5.88325% (ซึ่งเราใช้เป็นบรรทัดฐาน)
เลือกชิ้นงานอย่างสุ่มเพื่อการวัด (Randomly Sampling for Gage)
เราใช้พจน์ “random” เพื่อเป็นมาตรฐานในการเปรียบเทียบกับสิ่งที่เราทำไว้ในบทความส่วนที่ 1 และ 2 ซึ่งไม่ได้ให้ค่าประมาณที่ถูกต้องนัก

ในหลายๆครั้ง ที่คนทำการทดลองมักจะบอกผมว่า ไม่สามารถทำการสุ่มได้เพราะว่าชิ้นงานที่ได้มานั้นไม่ได้มีการแจกแจงแบบที่ควรจะเป็น
ชิ้นงานตัวอย่าง 10 ชิ้น มีการแจกแจงแบบที่ตั้งไว้หรือไม่
มาเปรียบเทียบสถานการณ์การเลือกชิ้นงานแบบ random กับ แบบ exact โดยถ้าเรามีพลังวิเศษทำการเลือกชิ้นงานมาได้ 10 ชิ้น เราจะได้การแจกแจงของชิ้นงานที่เกือบสมบูรณ์แบบ หมายความว่าเราได้กำจัดทิ้งผลกระทบของการสุ่ม (randomness) ออกไป

จะเห็นว่ามีบางอย่างที่แสดงไว้ชัดเจนเกี่ยวกับเรื่องการสุ่ม ที่มาจากการสุ่มตัวอย่าง (random sampling) ซึ่งมีผลกระทบมากต่อการประมาณค่า %Contribution โดยการการแจกแจงของรูปแบบการทดลองแบบ exact จะเห็นว่ามีการเบ้ (Skew) และความผันแปรน้อยกว่า ซึ่งทำให้การประเมินระบบการวัดทำได้ดีขึ้น ในการทำการทดลองแบบ exact นั้นไม่สามารถทำได้จริงในเกือบทุกๆกรณี เพราะว่าคุณไม่รู้ว่าระบบของคุณมีความคลาดเคลื่อน (error)เท่าไหร่ และนั้นทำให้ไม่สามารถทำให้เกิดการแจกแจงที่ถูกต้องได้ ซึ่งเป็นปัญหาโลกแตกเหมือนหาว่าไก่กับไข่อะไรเกิดก่อนกัน
สุ่มแบบ Uniform จากค่าช่วงของค่าชิ้นงานที่เป็นอยู่
มาต่อที่รูปแบบการสุ่มแบบที่ 2 เราจะทำการเปรียบเทียบ ได้ผลดังนี้

เราได้ผลแบบใหม่ จะเห็นได้ว่าความผันแปรลดลงแต่มี bias อย่างชัดเจน ในการทำแบบนี้เราจะดึงชิ้นงานแบบ uniform ตลอดช่วงของชิ้นงานซึ่งจะทำให้การประมาณค่านั้นมีความเสถียร(consistent) ขึ้น ทำให้ค่าประมาณที่ได้บ่งบอกว่าระบบการวัดนั้นดีมากกว่าที่ระบบนั้นเป็นจริง
สุ่มแบบ uniform ตลอดช่วงข้อกำหนดเฉพาะ
ผลที่ได้เป็นดังนี้

รูปแบบการสุ่มแบบนี้จะเห็นว่ามีค่า bias อย่างมาก ซึ่งทำให้การประเมินระบบการวัดที่ได้เป็น excellence คงไม่จำเป็นต้องบอกว่า ผลการประเมินนี้ไม่มีความถูกต้องเลย
การสุ่มชิ้นงานจากช่วงที่อยู่นอกข้อกำหนดเฉพาะ
รูปแบบสุดท้าย คือ เลือกชิ้นงานแบบสุ่ม และมีหนึ่งชิ้นที่เลือกจากช่วงที่อยู่นอกขอบเขตกำหนดเฉพาะ หมายความว่าจะมีจุดข้อมูล 2 จุด ออกนอกเขตกำหนดเฉพาะ จะมีผลแตกต่างอย่างชัดเจน แบบนั้นหรือไม่

จริงๆแล้วข้อมูล 2 จุดนั้นส่งให้เกิดผลที่แตกต่างไปอย่างมาก และทำไม่มีผลต่อการศึกษา ในกระบวนที่เราเลือกนี้มีค่า Ppk เท่ากับ 1 เป็นกระบวนการที่มีคุณภาพมาก ยิ่งทำให้ผลที่ได้มีความชัดเจนมากขึ้น ว่ารูปแบบการเลือกชิ้นงานแบบนี้ไม่เหมาะสม
ทำไมถึงได้จำลองรูปแบบการเลือกชิ้นงานแบบนี้
ถ้าคุณเรียนมาว่าจะต้องเลือกชิ้นงานอย่างสุ่ม คุณอาจจะสงสัยว่าแล้วทำไมยังมีหลายต่อหลายคนใช้วิธีการเลือกชิ้นงานตามรูปแบบที่กล่าวมา (หรือใกล้เคียงกับรูปแบบต่างๆนั้น) ในรูปแบบเหล่านั้นมีบางสิ่งที่คล้ายกันอยู่ รูปแบบทั้งหมดนั้นทำให้ผู้ประเมินสามารถประเมินระบบได้ตลอดช่วงค่าข้อมูลที่เป็นไปได้ อย่างไรก็ตามถ้าค่าที่คุณได้อยู่ระหว่าง 8.2 และ 8.3 รวมทั้งกระบวนการไม่อยู่ในการควบคุม คุณจะรู้ได้อย่างไรว่าคุณสามารถวัดชิ้นงานที่มีค่า 8.4 ถ้าคุณไม่เคยได้ประเมินเลยว่าระบบการวัดของคุณนั้นเคยไปถึงข้อมูลจุดนั้น
สำหรับคนที่เลือกรูปแบบการทดลองตามแบบที่กล่าวมาแล้วนั้น คงเคยคิดถึงประเด็นที่ว่ามาแล้วแต่ไม่ใช่การเลือกเครื่องมือที่ถูกต้องนัก Gage R&R คือการประเมินระบบความสามารถของเครื่องมือวัดเทียบกับกระบวนการในปัจจุบัน ในการประเมินระบบการวัดตลอดช่วงการใช้งานทั้งหมดจะต้องมีการใช้เครื่องมือสำหรับการศึกษา “bias and Linearity” ซึ่งมีใน minitab ในส่วนของคำสั่ง “gage Study” เครื่องมือนี้สร้างเพื่อศึกษา Bias ของระบบตลอดย่านการวัด (ดูว่าค่าวัดนั้นถูกต้องทั้งย่านการวัดค่าต่ำและค่าสูง) หรือ bias นั้นเกิดขึ้นต่างกันตามค่าวัด (ตัวอย่างเช่น วัดชี้นงานขนาดเล็ก แต่ขนาดที่ได้มีขนาดใหญ่กว่า และเมื่อวัดชิ้นงานขนาดใหญ่ค่าวัดที่อ่านได้มีขนาดเล็กที่กว่าควรจะเป็น)
ในการประเมินระบบการวัด ขอแนะนำว่าควรทำทั้งเรื่อง Bias and Linearity และ Gage R&R
รูปแบบการสุ่มแบบใดที่ควรเลือกใช้
ในตอนเริ่มต้นผมแนะนำให้ใช้รูปแบบ เลือกชิ้นงานแบบสุ่ม แต่จากที่อธิบายไว้จะเห็นว่าวิธีแบบ exact ให้ผลลัพธ์ที่ดีกว่า การใช้วิธี exact จะต้องรู้ว่าข้อมูลนั้นมีการแจกแจงแบบไหน (แม้การแจกแจงของข้อมูลนั้นจะรวมค่าความคลาดเคลื่อนด้วย) และเพื่อให้การวัดชิ้นงานอย่างถูกต้องต้องมั่นใจด้วยว่ามีการเลือกชิ้นงานที่ถูกต้อง (ซึ่งต้องไม่ลืมว่า การที่คุณจะรู้ว่าคุณว่าค่าได้ถูกต้องนั้นเป็นไปไม่ได้ เพราะไม่เช่นนั้น คุณจะทำการศึกษาเรื่อง Gage R&R ทำไม) หรือจะเรียกว่ามันไม่สามารถเป็นจริงได้
ดังนั้นสิ่งที่ดีที่สุดที่เราทำได้ คือ เลือกชิ้นงานอย่างสุ่ม แต่เราจะทำการตรวจสอบอีกครั้งโดยการหาค่าวัดเฉลี่ยของแต่ละชิ้นงานที่เลือกมาและทำการดูการแจกแจงค่าวัดว่าเหมาะสมหรือไม่ ถ้าการแจกแจงข้อมูลของ
กระบวนการเป็นการแจกแจงแบบปกติ แต่การแจกแจงของค่าวัดชิ้นงานแสดการแจกแจงมีความเบ้ นั้นอาจหมายความว่าชิ้นงานที่นำมาทดสออบอาจจะไม่ปกติ ซึ่งคุณอาจจะต้องมีเพิ่มชิ้นงานตัวอย่างในการทดสอบ
บทความต้นฉบับ : http://blog.minitab.com/blog/fun-with-statistics/gauging-gage-part-3-how-to-sample-parts
เนื้อหาบทความโดยบริษัท Minitab Inc. ประเทศสหรัฐอเมริกา
แปลและเรียบเรียงโดยสุวดี นําพาเจริญ และ ชลทิขา จํารัสพร, บริษัท โซลูชั่น เซ็นเตอร์ จํากัด webadmin@solutioncenterminitab.com

